Mathematics, mechanics, and a new kind of lecture
Geoffrey Burton, Professor Emeritus, Department of Mathematical Sciences
Professor Burton tracks Edward Fraenkel’s journey from aerodynamics research to pure mathematics teaching
Edward Fraenkel had an engineer's education, including the appropriate mathematics (of which he studied as much as possible), and this fitted him for his early career as an experimentalist at the Royal Aircraft Establishment, Farnborough. As his interests developed, he was drawn towards the theoretical and mathematical aspects of aerodynamics, culminating in a move into academia. Increasingly he found himself asking questions that could not be answered by the classical mathematical methods he had studied as a student and realised the necessity of him learning functional analysis and the modern theory of nonlinear partial differential equations, prompted especially by a sabbatical taken at the Courant Institute for Mathematical Sciences of New York University. In the United Kingdom, much of this material was not taught at universities, even in mathematics degrees, and in order both to educate himself and to benefit his students he set about preparing and delivering advanced lecture courses on these topics.
An example is Functional Analysis II, comprising highly specialised contents: introductory degree theory of functions in finite dimensions, its extension to infinite dimensions, fixed-point theory and its applications. The first page is typed, presumably for circulation to students, and lists three books for reference, followed by a characteristic admonishment: 'All three contain a number of mistakes; a large number in the case of ref.1. Apart from this, ref.1 is by far the easiest'.
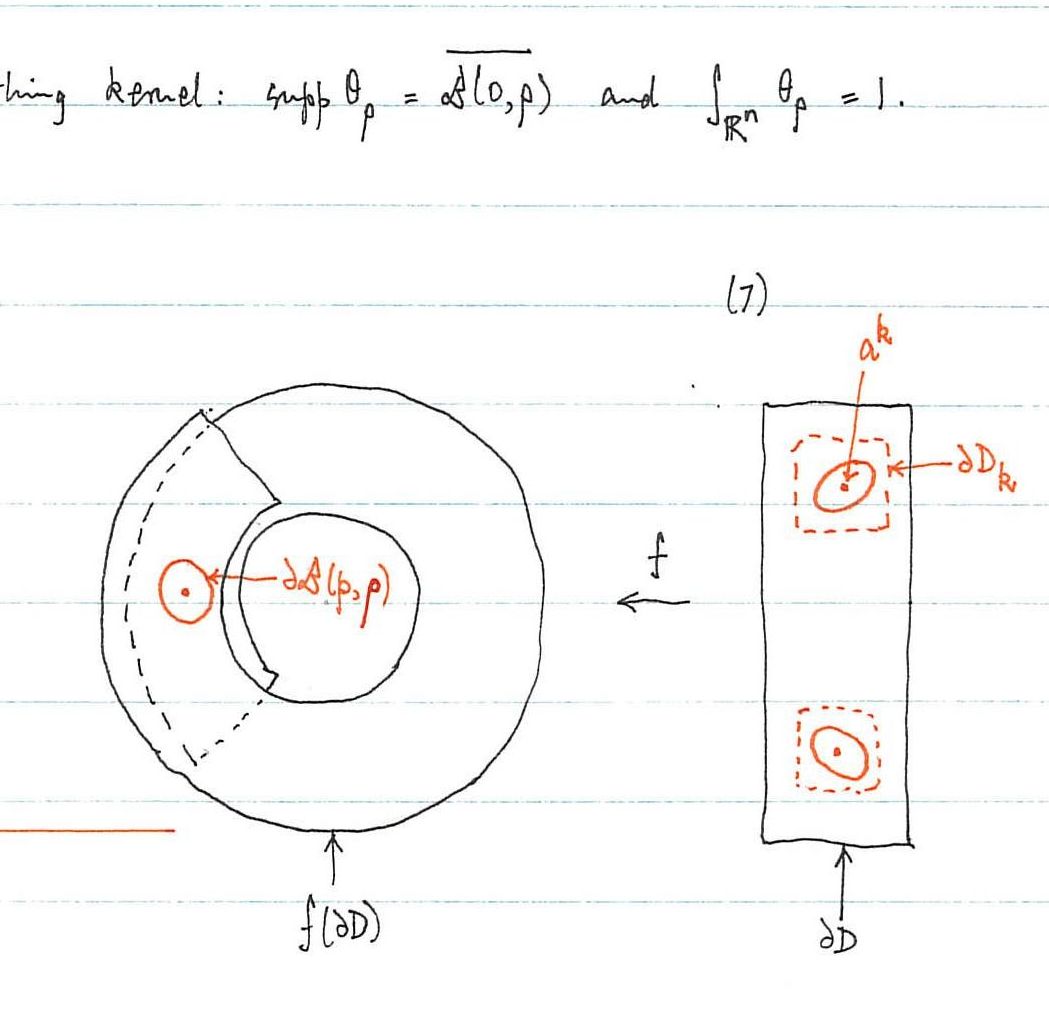
Thereafter the notes are written by hand, presumably for the lecturer's sole use, immaculate, nonetheless. Neat freehand diagrams of regions, graphs, curves and geometric figures, illustrate the concepts under discussion. Sections of the course are numbered systematically A, B, C, D, E, with subsections A.1º, A.2º, A.3º, etc. and theorems have numbers appropriate to their section, e.g. Theorem B11, having corollaries numbered B11’ and B11’’. Headings are underlined using a ruler, as also are terms being defined, and proper names are written in small capitals.
The arguments are presented in great detail, suggesting not only a great understanding of the needs of the students, but also an expositor proceeding with caution in unfamiliar territory and needing to be absolutely sure of the foundations. This may be due in part to his having learned the subject matter in his late thirties, and perhaps also to mindfulness (and awe) of the fastidious standards of his father, a distinguished classical scholar.
The contents of the course are presented as pure mathematics, with an application to mechanics near the end to prove the utility of the foregoing theory. The destination of Fraenkel's intellectual journey, from Scientific Officer at Farnborough to Professor of Pure Mathematics at Bath, is exemplified by this course, as it is even more by his later published research, which addresses significant questions in fluid mechanics as its object by methods drawn from functional analysis, rather than using examples as mere illustrations of theory.