 Credits: Credits:
| 6 |
 Level: Level:
| Honours (FHEQ level 6) |
 Period: Period: |
Semester 1
|
 Assessment: Assessment:
| EX 100% |
 Supplementary Assessment: Supplementary Assessment: | MA30041 Mandatory extra work (where allowed by programme regulations) |
 Requisites: Requisites:
| Before taking this unit you must take MA20218 |
 Description: Description:
| Aims & Learning Objectives:
Aims - This core course is intended to be an elementary and accessible introduction to the theory of metric spaces and the topology of Rn for students with both pure and applied interests.
Objectives - While the foundations will be laid for further studies in Analysis and Topology, topics useful in applied areas such as the Contraction Mapping Principle will also be covered. Students will know the fundamental results listed in the syllabus and have an instinct for their utility in analysis and numerical analysis.
Content:
Definition and examples of metric spaces. Convergence of sequences. Continuous maps and isometries. Sequential definition of continuity. Subspaces and product spaces. Complete metric spaces and the Contraction Mapping Principle. Picard's Theorem for 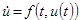 . Sequential compactness, Bolzano-Weierstrass theorem and applications. Open and closed sets (with emphasis on Rn). Closure and interior of sets. Topological approach to continuity and compactness (with statement of Heine-Borel theorem). Equivalence of Compactness and sequential compactness in metric spaces. Connectedness and path-connectedness. Metric spaces of functions: C[0,1] is a complete metric space. . Sequential compactness, Bolzano-Weierstrass theorem and applications. Open and closed sets (with emphasis on Rn). Closure and interior of sets. Topological approach to continuity and compactness (with statement of Heine-Borel theorem). Equivalence of Compactness and sequential compactness in metric spaces. Connectedness and path-connectedness. Metric spaces of functions: C[0,1] is a complete metric space. |
 Programme availability: Programme availability:
|
MA30041 is Compulsory on the following programmes:
Department of Physics
- USXX-AFM01 : MSci (hons) Mathematics and Physics (Full-time) - Year 3
MA30041 is Optional on the following programmes:
Department of Computer Science
- USCM-AFB01 : BSc Computing (Full-time) - Year 3
- USCM-AKB01 : BSc Computing (Full-time with Thick Sandwich Placement) - Year 4
- USCM-AFB13 : BSc (hons) Computer Science with Mathematics (Full-time) - Year 3
- USCM-AKB14 : BSc (hons) Computer Science with Mathematics (Full-time with Thick Sandwich Placement) - Year 4
- USCM-AAB14 : BSc (hons) Computer Science with Mathematics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
Department of Mathematical Sciences
- USMA-AFB15 : BSc (hons) Mathematical Sciences (Full-time) - Year 3
- USMA-AKB16 : BSc (hons) Mathematical Sciences (Full-time with Thick Sandwich Placement) - Year 4
- USMA-AAB16 : BSc (hons) Mathematical Sciences with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
- USMA-AFB13 : BSc (hons) Mathematics (Full-time) - Year 3
- USMA-AKB14 : BSc (hons) Mathematics (Full-time with Thick Sandwich Placement) - Year 4
- USMA-AFB01 : BSc (hons) Mathematics and Statistics (Full-time) - Year 3
- USMA-AKB02 : BSc (hons) Mathematics and Statistics (Full-time with Thick Sandwich Placement) - Year 4
- USMA-AAB02 : BSc (hons) Mathematics and Statistics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
- USMA-AAB14 : BSc (hons) Mathematics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
- USMA-AFB05 : BSc (hons) Statistics (Full-time) - Year 3
- USMA-AKB06 : BSc (hons) Statistics (Full-time with Thick Sandwich Placement) - Year 4
- USMA-AAB06 : BSc (hons) Statistics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
- USMA-AFM14 : MMath Mathematics (Full-time) - Year 3
- USMA-AFM14 : MMath Mathematics (Full-time) - Year 4
- USMA-AAM15 : MMath Mathematics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
- TSMA-AFM09 : MSc Mathematical Sciences (Full-time) - Year 1
- TSMA-APM09 : MSc Mathematical Sciences (Part-time) - Year 1
- TSMA-APM09 : MSc Mathematical Sciences (Part-time) - Year 2
Department of Physics
- USXX-AFB03 : BSc (hons) Mathematics and Physics (Full-time) - Year 3
- USXX-AKB04 : BSc (hons) Mathematics and Physics with Placement (Full-time with Thick Sandwich Placement) - Year 4
- USXX-AAB04 : BSc (hons) Mathematics and Physics with Study Year Abroad (Full-time with Study Year Abroad) - Year 4
|

