 Academic Year: Academic Year: | 2017/8 |
 Owning Department/School: Owning Department/School: | Department of Mathematical Sciences |
 Credits: Credits: | 6 [equivalent to 12 CATS credits] |
 Notional Study Hours: Notional Study Hours: | 120 |
 Level: Level: | Honours (FHEQ level 6) |
 Period: Period: |
- Semester 1
|
 Assessment Summary: Assessment Summary: | EX 100% |
 Assessment Detail: Assessment Detail: | |
 Supplementary Assessment: Supplementary Assessment: |
- Like-for-like reassessment (where allowed by programme regulations)
|
 Requisites: Requisites: |
Before taking this module you must take MA20218
|
 Description: Description:
| Aims & Learning Objectives:
Aims - This core course is intended to be an elementary and accessible introduction to the theory of metric spaces and the topology of Rn for students with both pure and applied interests.
Objectives - While the foundations will be laid for further studies in Analysis and Topology, topics useful in applied areas such as the Contraction Mapping Principle will also be covered. Students will know the fundamental results listed in the syllabus and have an instinct for their utility in analysis and numerical analysis.
Content:
Definition and examples of metric spaces. Convergence of sequences. Continuous maps and isometries. Sequential definition of continuity. Subspaces and product spaces. Complete metric spaces and the Contraction Mapping Principle. Picard's Theorem for 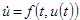 . Sequential compactness, Bolzano-Weierstrass theorem and applications. Open and closed sets (with emphasis on Rn). Closure and interior of sets. Topological approach to continuity and compactness (with statement of Heine-Borel theorem). Equivalence of Compactness and sequential compactness in metric spaces. Connectedness and path-connectedness. Metric spaces of functions: C[0,1] is a complete metric space. . Sequential compactness, Bolzano-Weierstrass theorem and applications. Open and closed sets (with emphasis on Rn). Closure and interior of sets. Topological approach to continuity and compactness (with statement of Heine-Borel theorem). Equivalence of Compactness and sequential compactness in metric spaces. Connectedness and path-connectedness. Metric spaces of functions: C[0,1] is a complete metric space.
|
 Programme availability: Programme availability: |
MA30041 is Compulsory on the following programmes:
Department of Physics
- USXX-AAM01 : MSci(Hons) Mathematics and Physics with Study year abroad (Year 4)
- USXX-AKM01 : MSci(Hons) Mathematics and Physics with Year long work placement (Year 4)
MA30041 is Optional on the following programmes:
Department of Mathematical Sciences
- USMA-AAB16 : BSc(Hons) Mathematical Sciences with Study year abroad (Year 4)
- USMA-AKB16 : BSc(Hons) Mathematical Sciences with Year long work placement (Year 4)
- USMA-AAB14 : BSc(Hons) Mathematics with Study year abroad (Year 4)
- USMA-AKB14 : BSc(Hons) Mathematics with Year long work placement (Year 4)
- USMA-AKM15 : MMath(Hons) Mathematics with Year long work placement (Year 4)
- USMA-AAB02 : BSc(Hons) Mathematics and Statistics with Study year abroad (Year 4)
- USMA-AKB02 : BSc(Hons) Mathematics and Statistics with Year long work placement (Year 4)
- USMA-AAB06 : BSc(Hons) Statistics with Study year abroad (Year 4)
- USMA-AKB06 : BSc(Hons) Statistics with Year long work placement (Year 4)
Department of Physics
- USXX-AAB04 : BSc(Hons) Mathematics and Physics with Study year abroad (Year 4)
- USXX-AKB04 : BSc(Hons) Mathematics and Physics with Year long work placement (Year 4)
|

